Book notes
Overview
一天中密西西比河的流量是多少?
作者估算:河口宽度大约 1 mile,大约 1/250 英里深,他猜测流速是 5mile 每小时或 120mile 每天。
1mile * 1/250mile * 120 miles/day = 1/2 mile3/day
基本技巧
两个答案好于一个
估算中密西西比河的流域是 1000 × 1000 miles, 一年雨量大约 1 英尺,(1/5000 英里每年)。 1000miles * 1000miles * 1/5000 mile/year = 200 mile3/year 200mile3/year/400days/year = 1/2 mile3/day
快速检查
- Rule1: 相加的单位与原来一样。
- Rule2: 相乘的单位是单位的相乘。
经验法则
72 法则。
假如一笔钱以年利率百分比 r 存 y 年。如果 r×y=72,那么钱将成 2 倍。这个估算大体正确,存 1000 以 6%的年利率存 12 年之后为 2012.
72 法则对估算指数增长非常实用。双倍对于程序员来说很熟悉:210=1024,10 倍双倍就是 1thousand,20 个双倍就是 1million。
假如一个指数型复杂度的程序花 10 秒解决一个 n=40 的问题,每把 n 增加 1 就增加 12%的运行时间。72 法则告诉我们,运行时间成 2 倍当 n 增加 6,也就是 1000 倍(210)当 n 增加 60(6*10)。所以当 n=100 时,程序花 10,000 秒,也就几小时。当 n 增加到 160,时间成为 107 秒,那这时间大约是多少呢?
很难记住一年的时间是 3.155×107 秒,另一方面,很难忘记 Tom Duff 的实用经验准则,1%多的误差:
$\pi$ 秒是 1 纳世纪。 ($\pi$ seconds is a nanocentury.)练习
不断练习提高自己的估算技巧。
书中估算密西西比河的流量并不是特别技巧好,比如直接估测出流速是 5mile 每小时,很难直观想出这个数字。
推荐《这也能想到?——巧妙解答无厘头问题》 这本书,全书都是估算题目,
- 明白估算的目标精确度只需要达到一个数量级,和真实数据不超过 10 倍就是比较好的估算。
- 估算一个东西的范围的关键是几何平均数。比如这里流量最小 1mile 每小时,最大 10mile 每小时,那么估算它为 3mile 每小时(几何平均)。比如地球的密度,比水大,比铁小,取它们的几何平均。
利特尔法则(Little’s law)
在一个稳定系统中长期平均存在的用户数是平均用户离开系统的速率与用户平均在系统的时间的乘积。
例如:一个地方能容纳 60 个人,你准备呆在那大约 3 小时,所以人们进入这个地方的速率是 20 个每小时。现在队伍中有 20 个人,那么意味着你将等 1 小时左右。
或多用户系统的回复时间公式:假定用户连接到回复时间是 r 的系统中的平均思考时间是 z,每个用户或思考或等待系统回复,系统中的任务数大约固定在 n,可以测得系统的吞吐量是 x(每时间单位的任务数),由 Little’s law 得, n=x*(z+r)。可以算得 r=n/x - z。
Problems
1
密西西比河的流速大概是 5mile 每小时或 120mile 每天,Passaic River 应该是 200miles 每天。
3
软盘有 1.44Mbytes,
一秒中最少可以打 1byte,最多 10bytes,也就是每分钟最少 60bytes 和最多 600bytes,它们的几何平均是 200byte,认为大约每分钟打字 200byte, 1.44*106/200=7200 minutes。
5
证明 72 法则。
若(1+x%)N = 2,证明 x*N 约等于 72
(1+x%)N=2 ==> N*ln(1+x%)=ln2
对 ln(1+x)泰勒展开是 ln(1+x) = x-(x2)/2 + (x3)/3 + …
N*ln(1+x%)=ln2 ==> N*x = ln2 * 100 = 69.3
因为忽略了-(x2)/2 这个项,所以 N*x 约等于 72。
6
72/1.33=54, 所以到 2052 年人口是 2 倍,就是 5.9×2=11.8 billion。那么 2050 年大约就是 11.5 billion。
10
估算城市的死亡率。
假定大家平均生命是 70 年,根据 Little’s law,那么每年的死亡率就是 1/70=1.4%的城市人口。
11
证明利特尔法则(Little’s law)。
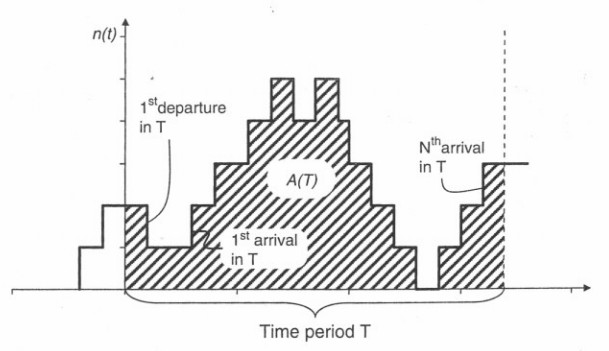
时间 T 进入个数为 N(T),那么到达速率 λ(T) = N(T)/T;
时间 T 离开个数为 C(T),那么离开速率 X = C(T)/T;
系统中,时间 T 中堆积的个数平均为阴影部分 A(T),那么平均等待的个数为 L(T) = A(T)/T;
时间 T 离开个数为 C(T),时间 T 中堆积的个数 A(T),那么每个的等待时间是 W(T)=A(T)/C(T)。
可以得到 L(T)=C(T)W(T),均衡系统λ(T)=C(T),即 L(T)=λ(T)W(T)。
完善的数学证明这里: http://www.columbia.edu/~ks20/stochastic-I/stochastic-I-LL.pdf
12
美国报纸说 25 美分的硬币平均寿命是 30 年。你如何检测这个声明?
硬币制造厂每年平均最小为每个人制造 1 枚 25 美分的硬币,最多不会超过 100 枚,那么几何平均就是 10 枚,加入它的平均寿命是 30 年,那么平均每人就有 300 枚 25 美分的硬币在手里,算上手头,家里抽屉,公司抽屉所有的 25 美分,应该不会超过 300 枚,所以这个声明的数字有点偏高。